14. Other Classic ML Models (1)

Naïve Bayes

Naïve Bayes Models

머신러닝에서 아마도 가장 일반적이고 단순한 Bayesian network 모델
Naïve Bayes(나이브 베이즈) 모델은 클래스 변수(class variable)가 주어졌을 때, 특정 특성의 값이 다른 특성의 값과 (조건부적으로) independent하다고 가정함.
실제로는 조건부 독립 가정이 엄격하게 사실이 아니더라도 잘 작동하는 경우가 많음.

Text Classification with Naïve Bayes

텍스트 분류 작업에 Naïve Bayes 모델을 사용하는 방법
작업: 주어진 텍스트가 어떤 클래스(class)나 카테고리(\text{category})에 속하는지 결정
"원인" = $\text{Category}$ 변수, "결과" 변수 = 특정 키워드의 존재 여부 ( $\text{HasWord}_i$ )
예제 문장 (신문 기사)
- “Stocks rallied on Monday, with major indexes gaining 1% as optimism persisted over the first quarter earnings season.” (business)
- “Heavy rain continued to pound much of the east coast on Monday, with flood warnings issued in New York City and other locations.” (weather)
작업: 각 문장을 주요 섹션 (news, sports, business, weather, or entertainment)으로 분류
Naïve Bayes 모델은 사전 확률(prior probabilities) $P(\text{Category})$ 와 조건부 확률(conditional probabilities) $P(\text{HasWord}_i~|~\text{Category})$ 로 구성됨.
사후 확률(Posterior probability)은 사전 확률과 likelihood(가능도) (조건부 확률)의 곱에 비례

\begin{aligned} & P(\text{Category} | \text{HasWord}_{w1},~ \text{HasWord}_{w2},~ \dots,~ \text{HasWord}_{wn}) \\ & = \frac{P(\text{HasWord}_{w1},~ \text{HasWord}_{w2},~ \dots,~ \text{HasWord}_{wn} | \text{Category}) P(\text{Category})}{P(\text{HasWord}_{w1},~ \text{HasWord}_{w2},~ \dots,~ \text{HasWord}_{wn})} \\ & \propto P(\text{HasWord}_{w1},~ \text{HasWord}_{w2},~ \dots,~ \text{HasWord}_{wn} | \text{Category}) P(\text{Category}) \\ & = P(\text{HasWord}_{w1} | \text{Category}) \cdots P(\text{HasWord}_{wn} | \text{Category}) P(\text{Category}) \\ & = \prod_{i} P(\text{HasWord}_{wi} | \text{Category}) P(\text{Category}) \end{aligned}

Naïve Bayes 가정: 각 단어의 존재는 카테고리가 주어졌을 때 조건부 독립

각 카테고리 $c$ 에 대해

$P(\text{Category} = c)$ 는 이전에 본 모든 문서 중 카테고리 $c$ 의 비율로 추정
예: 9%가 날씨 기사면 $P(\text{Category} = \text{weather}) = 0.09$
$P(\text{HasWord}_i~|~\text{Category})$ 는 각 카테고리의 문서 중 단어 $i$ 를 포함하는 비율로 추정
예: 비즈니스 기사의 37%가 "stocks"를 포함하면 $P(\text{HasWord}_{\text{"stocks"}} = \text{true}~|~\text{Category} = \text{business}) = 0.37$

새 문서 분류

키워드 확인 후, 공식을 적용하여 카테고리에 대한 사후 확률 분포(posterior probability distribution)를 얻음.
하나의 카테고리만 예측해야 하는 경우, 가장 높은 사후 확률을 가진 것을 선택

Naïve Bayes 모델은 단어가 문서 범주에 따라 결정되는 빈도로 문서에서 독립적으로 발생한다고 가정

이 독립 가정은 실제로는 위배
예: "first quarter" 구문은 "first" $\times$ "quater"가 제안하는 것보다 비즈니스 (or 스포츠) 기사에서 더 자주 발생

이러한 오류에도 불구하고, 가능한 카테고리의 순위(ranking)는 종종 매우 정확

Naïve Bayes 모델은 언어 결정, 문서 검색, 스팸 필터링(spam filtering) 및 기타 분류 작업에 널리 사용
실제 사후 확률 값이 중요한 작업(예: 의료 진단)의 경우, 신경망(neural networks)과 같은 더 정교한 모델을 선호

Decision Trees 결정 나무?

Attribute values의 벡터를 단일 출력 값("decision")에 매핑하는 함수의 표현
결정 트리(Decision tree)는 root에서 시작하여 leaf에 도달할 때까지 일련의 테스트를 수행하여 결정에 도달
내부 노드(Internal node): 입력 속성 중 하나에 대한 테스트
가지(Branches): 속성의 가능한 값
리프 노드(Leaf nodes): 함수가 반환할 값 지정
입력 및 출력 값은 이산형(discrete) 또는 연속형(continuous)일 수 있음.
현재: 이산형 입력, Boolean (true/false) 출력 $\rightarrow$ Boolean (=binary) classification(불리언 (=이진) 분류)
표기법(Notation): $j$ 는 예제 인덱스 ( $\mathbf{x}^j$ 는 $j$ 번째 예제의 입력 벡터,~ $y^j$ 는 출력),~ $x_{j,i}$ 는 $j$ 번째 예제의 $i$ 번째 속성

Example Problem: Restaurant Waiting

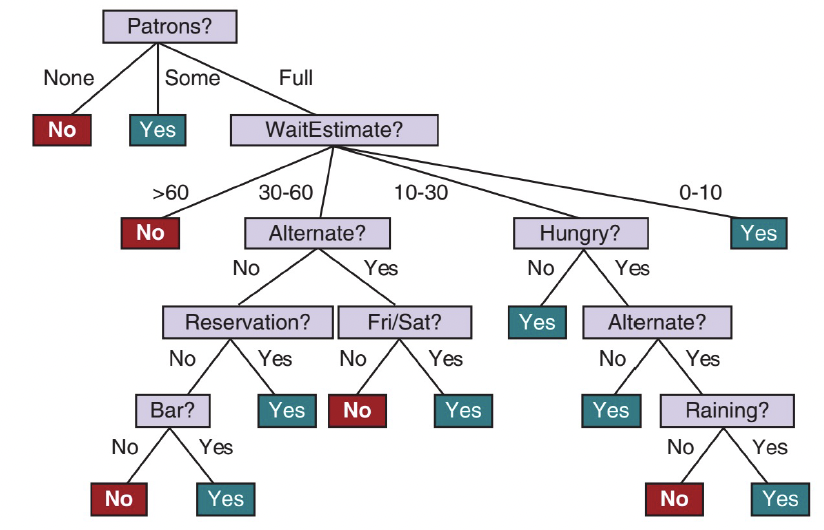
문제: 식당에서 테이블을 기다릴지 결정하는 문제
출력 $y$ : Boolean 변수 $WillWait$ (기다릴 경우 true)
입력 $\mathbf{x}$ $x$ : 10개 속성 값의 벡터 (모두 이산형 값)
1. $Alternate$ : 근처에 적절한 대안 식당이 있는지
2. $Bar$ : 기다릴 수 있는 편안한 바(bar) 공간이 있는지
3. $Fri/Sat$ : 금요일 또는 토요일인지 (true)
4. $Hungry$ : 지금 배가 고픈지
5. $Patrons$ : 식당 안 사람 수 ( $None$ , $Some$ , $Full$ )
6. $Price$ : 식당 가격대 ($$$, $$$$, $$$$$)
7. $Raining$ : 밖에 비가 오는지
8. $Reservation$ : 예약을 했는지
9. $Type$ : 식당 종류 (French, Italian, Thai, or burger)
10. $WaitEstimate$ : 호스트의 예상 대기 시간 (0–10, 10–30, 30–60, or >60 분)
12개 예제 세트가 그림에 표시
- 데이터가 매우 적음: $2^6 \times 3^2 \times 4^2 = 9216$ 가지 가능한 입력 조합 중 12개만 주어짐
- 12개의 증거(evidence)만으로 누락된 9,204개의 출력 값을 추측해야 함.

Example	Alt	Bar	Fri	Hun	Pat	Price	Rain	Res	Type	Est	WillWait
$x_1$	Yes	No	No	Yes	Some	$$$	No	Yes	French	0–10	$y_1 = \text{Yes}$
$x_2$	Yes	No	No	Yes	Full	$	No	No	Thai	30–60	$y_2 = \text{No}$
$x_3$	No	Yes	No	No	Some	$	No	No	Burger	0–10	$y_3 = \text{Yes}$
$x_4$	Yes	No	Yes	Yes	Full	$$$	Yes	No	Thai	10–30	$y_4 = \text{Yes}$
$x_5$	Yes	No	Yes	No	Full	$$$	No	Yes	French	>60	$y_5 = \text{No}$
$x_6$	No	Yes	No	Yes	Some	$$	Yes	Yes	Italian	0–10	$y_6 = \text{Yes}$
$x_7$	No	Yes	No	No	None	$	Yes	No	Burger	0–10	$y_7 = \text{No}$
$x_8$	No	No	No	Yes	Some	$$	Yes	Yes	Thai	0–10	$y_8 = \text{Yes}$
$x_9$	No	Yes	Yes	No	Full	$	Yes	No	Burger	>60	$y_9 = \text{No}$
$x_{10}$	Yes	Yes	Yes	Yes	Full	$$$	No	Yes	Italian	10–30	$y_{10} = \text{No}$
$x_{11}$	No	No	No	No	None	$	No	No	Thai	0–10	$y_{11} = \text{No}$
$x_{12}$	Yes	Yes	Yes	Yes	Full	$	No	No	Burger	30–60	$y_{12} = \text{Yes}$

A Decision Tree for Restaurant Waiting

alt text

Learning Decision Trees from Examples

목표: 학습 데이터(training data)와 일치(consistent)하면서 가능한 가장 작은 Decision tree를 찾는 것

보장된 가장 작은 트리를 찾는 것은 난해(intractable)함.
간단한 휴리스틱을 사용하여 가장 작은 트리에 가까운 것을 효율적으로 찾을 수 있음.
LEARN-DECISION-TREE 알고리즘은 탐욕적 분할 정복(greedy divide-and-conquer) 전략을 채택
항상 가장 중요한(most important) 속성을 먼저 테스트한 다음, 테스트 결과로 정의되는 더 작은 하위 문제(subproblems)를 재귀적으로 해결
"가장 중요한 속성": 예제의 분류에 가장 큰 차이를 만드는 속성

목표: 적은 수의 테스트로 올바른 분류에 도달 (트리의 모든 경로가 짧고 트리가 얕음)

그림 (a)는 $Type$ 이 좋지 않은 속성임을 보여줌 (4개의 결과 모두 양성/음성 예제가 동일)
그림 (b)는 $Patrons$ 가 상당히 중요한 속성임을 보여줌 ( $None$ 또는 $Some$ 인 경우, 명확한 답( $No$ 또는 $Yes$ )을 얻음)

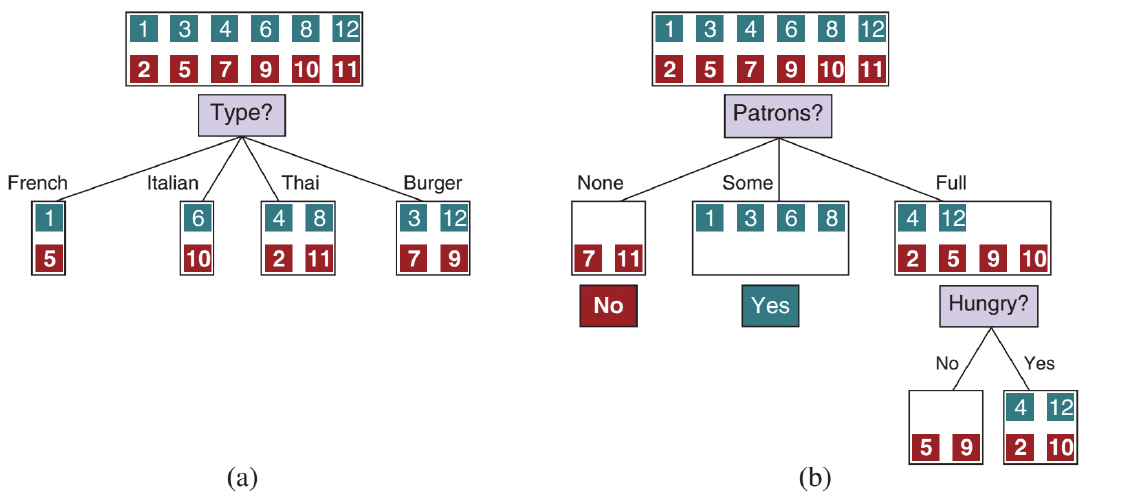
alt text

값이 $Full$ $F u ll$ 이면, 혼합된 예제 세트가 남음. 이러한 재귀적 하위 문제(recursive subproblems)에 대한 4가지 경우
1. 남은 예제가 모두 양성 (또는 모두 음성)인 경우: 완료 ( $Yes$ 또는 $No$ 로 답함). (b)의 $None$ 및 $Some$ 가지 예시
2. 일부 양성 및 일부 음성 예제가 있는 경우: 이들을 분할할 최상의 속성을 선택함. (b)에서 남은 예제를 분할하기 위해 $Hungry$ 가 사용
3. 남은 예제가 없는 경우: 이 속성 값 조합에 대해 관찰된 예제가 없음을 의미. 부모 노드(parent) 구성에 사용된 예제 세트에서 가장 일반적인 출력 값을 반환
4. 속성은 남지 않았지만 양성 및 음성 예제가 모두 있는 경우: 데이터의 오류나 노이즈(noise), 비결정론적(nondeterministic) 도메인, 또는 구별할 수 있는 속성을 관찰할 수 없기 때문일 수 있음. 남은 예제 중 가장 일반적인 출력 값을 반환

`LEARN-DECISION-TREE` Algorithm

alt text

샘플 training set에 대한 학습 알고리즘의 출력
트리는 내부 노드의 테스트, 가지의 속성 값, 리프 노드의 출력 값으로 구성
학습 알고리즘은 $Raining$ 과 $Reservation$ 에 대한 테스트를 포함하지 않음 (모든 예제를 분류하는 데 필요하지 않기 때문)

Choosing Attribute Tests

Decision tree learning algorithm은 가장 높은 IMPORTANCE를 가진 속성을 선택
Entropy 개념을 사용하여 정의되는 information gain을 사용하여 IMPORTANCE를 측정

Entropy 복습

Random variable의 불확실성 척도
값 $x$ $x$ 가 확률 $P(x)$ $P (x)$ 를 갖는 확률변수 $X$ $X$ 의 엔트로피
- $H(X) = -\sum_{x} P(x) \log_2 P(x)$
공정한 동전 던지기 엔트로피 = 1 bit
확률 $q$ 로 true인 boolean 확률변수의 엔트로피 $B(q)$ : $B(q) = -(q \log_2 q + (1-q) \log_2(1-q))$
$p$ 개의 positive example과 $n$ 개의 negative example을 포함하는 training set에서, 전체 세트에 대한 출력 변수의 엔트로피는 $H(Output) = B(\frac{p}{p+n})$
식당 training set: $p = n = 6$ 이므로, 해당 엔트로피는 $B(0.5)$ 즉 1 bit
속성 $A$ 에 대한 테스트 결과는 정보를 제공하여 전체 엔트로피를 감소시킴
$d$ 개의 고유한 값을 가진 속성 $A$ 는 training set $E$ 를 $E_1,~\dots,~E_d$ 부분집합(subsets)으로 나눔
각 부분집합 $E_k$ 는 $p_k$ 개의 positive example과 $n_k$ 개의 negative example을 가지며, 해당 가지를 따르면 $B(\frac{p_k}{p_k+n_k})$ 비트의 추가 정보가 필요
속성 $A$ 를 테스트한 후 남은 expected entropy
$Remainder(A) = \sum_{k=1}^{d} \frac{p_k + n_k}{p + n} B(\frac{p_k}{p_k+n_k})$

속성 $A$ 테스트로 인한 information gain

$Gain(A) = B(\frac{p}{p+n}) - Remainder(A)$
$Gain(A)$ 가 IMPORTANCE 함수를 구현함
$Gain(Patrons) = 1 - [\frac{2}{12} B(\frac{0}{2}) + \frac{4}{12} B(\frac{4}{4}) + \frac{6}{12} B(\frac{2}{6})] \approx 0.541$ bits
$Gain(Type) = 1 - [\frac{2}{12} B(\frac{1}{2}) + \frac{2}{12} B(\frac{1}{2}) + \frac{4}{12} B(\frac{2}{4}) + \frac{4}{12} B(\frac{2}{4})] = 0$ bits
$Patrons$ 가 분할하기 더 좋은 속성이라는 직관을 확인시켜 줌
$Patrons$ 는 모든 속성 중 최대 information gain을 가지므로 decision tree learning 알고리즘에 의해 root로 선택됨.