- 주어진 query 평가를 위한 대안적 방법들
- 동등한(Equivalent) 표현식
- 각 연산을 위한 다른 알고리즘
- Query 예시: Music 학부 강사의 이름과 그들이 가르치는 과목의 제목 검색
- Πname, title(σdept_name= ’Music’(instructor⋈(teaches⋈Πcourse_id, title(course))))
- Evaluation plan: 각 연산에 사용되는 알고리즘 및 연산 실행 방식 (materialized/pipelined) 정의
- Query에 대한 evaluation plan 간의 비용 차이는 막대할 수 있음 (예: 초 vs. 일)
- 비용 기반 query 최적화 단계
- 논리적으로 동등한(equivalent) 표현식 생성 (동등성 규칙(equivalence rules) 사용)
- 대안적 query plan을 얻기 위해 결과 표현식에 주석(annotate) 추가
- 추정된 비용에 기반하여 가장 저렴한 plan 선택
- Plan 비용 추정 기반
- Relation에 대한 통계 정보 (예: tuple 수, 속성의 distinct 값 수)
- 중간 결과에 대한 통계 추정 (복잡한 표현식 비용 계산용)
- 알고리즘에 대한 비용 공식 (통계 사용)
- 두 관계 대수(relational algebra) 표현식이 모든 legal한 데이터베이스 instance에서 동일한 tuple 집합을 생성하면 동등(equivalent)하다고 함 (Tuple 순서 무관)
- SQL에서 입출력은 tuple의 multiset (중복 허용 집합)
- Multiset 버전의 관계 대수에서 두 표현식이 모든 legal한 데이터베이스 instance에서 동일한 multiset을 생성하면 동등하다고 함
- Equivalence rule: 두 형태의 표현식이 동등함을 의미 (상호 교체 가능)
- Conjunctive selection 연산은 개별 selection의 sequence로 분해 가능 (cascade of σ)
- σθ1∧θ2(E)≡σθ1(σθ2(E))
- Selection 연산은 교환 가능(commutative, 교환법칙)
- σθ1(σθ2(E))≡σθ2(σθ1(E))
- Projection 연산 sequence에서는 마지막 하나만 필요
- ΠL1(ΠL2(…(ΠLn(E))…))≡ΠL1(E), (단, L1⊆L2⋯⊆Ln)
- Selection은 Cartesian product 및 theta join과 결합 가능
- a. σθ(E1×E2)≡E1⋈θE2
- b. σθ1(E1⋈θ2E2)≡E1⋈θ1∧θ2E2
- Theta join (및 natural join)은 교환 가능
- E1⋈θE2≡E2⋈θE1
- (a) Natural join은 결합 가능(associative, 결합법칙)
- (E1⋈E2)⋈E3≡E1⋈(E2⋈E3)
- (b) Theta join의 결합 법칙
- (E1⋈θ1E2)⋈θ2∧θ3E3≡E1⋈θ1∧θ3(E2⋈θ2E3) (단, θ2는 E2,E3의 속성만 포함)
- Selection 연산은 다음 두 조건 하에 theta join에 분배 가능
- (a) θ0의 모든 attribute가 join 되는 표현식 중 하나(E1)의 속성만 포함
- σθ0(E1⋈θE2)≡(σθ0(E1))⋈θE2
- (b) θ1이 E1의 속성만, θ2가 E2의 속성만 포함
- σθ1∧θ2(E1⋈θE2)≡(σθ1(E1))⋈θ(σθ2(E2))
- Projection 연산은 theta join에 다음과 같이 분배 가능
- (a) L1,L2가 각각 E1,E2의 attribute이고 θ가 L1∪L2의 속성만 포함
- ΠL1∪L2(E1⋈θE2)≡ΠL1(E1)⋈θΠL2(E2)
- (b) 일반적인 경우 (E1⋈θE2), L1⊆E1,L2⊆E2. L3는 E1의 attribute (join 조건 θ에 포함되지만 L1∪L2에는 미포함), L4는 E2의 attribute (join 조건 θ에 포함되지만 L1∪L2에는 미포함)
- ΠL1∪L2(E1⋈θE2)≡ΠL1∪L2(ΠL1∪L3(E1)⋈θΠL2∪L4(E2))
- 집합 연산 union(∪)과 intersection(∩)은 교환 가능 (Set difference(−)는 아님)
- Set union과 intersection은 결합 가능
- Selection 연산은 ∪, ∩, − 에 분배 가능
- a. σθ(E1∪E2)≡σθ(E1)∪σθ(E2)
- b. σθ(E1∩E2)≡σθ(E1)∩σθ(E2)
- c. σθ(E1−E2)≡σθ(E1)−σθ(E2)
- d. σθ(E1∩E2)≡σθ(E1)∩E2 (∪ 에는 성립 안 함)
- e. σθ(E1−E2)≡σθ(E1)−E2
- Projection 연산은 union에 분배 가능 (단, E1,E2 schema 동일)
- ΠL(E1∪E2)≡(ΠL(E1))∪(ΠL(E2))
- Selection을 가능한 한 빨리 수행하면 join할 relation의 크기 감소
- Query 예
- Πname, title(σdept_name= ’Music’(instructor⋈(teaches⋈Πcourse_id, title(course))))
- 규칙 7a를 이용한 변환
- Πname, title(σdept_name= ’Music’(instructor)⋈(teaches⋈Πcourse_id, title(course)))
- Query: "2017년에 강의를 담당한 음악학과 소속 모든 교수진의 성명을 해당 교수진이 담당한 강의 제목과 함께 찾아주세요."
- Πname, title(σdept_name= ’Music’∧year=2017(instructor⋈(teaches⋈Πcourse_id, title(course))))
- Join associatively (규칙 6a) 변환
- Πname, title(σdept_name= “Music”∧year=2017((instructor⋈teaches)⋈Πcourse_id, title(course)))
- 두 번째 형태는 'selection 조기 수행' 규칙 적용 기회 제공 (규칙 7a, 7b)
- σdept_name = “Music”(instructor)⋈σyear = 2017(teaches)
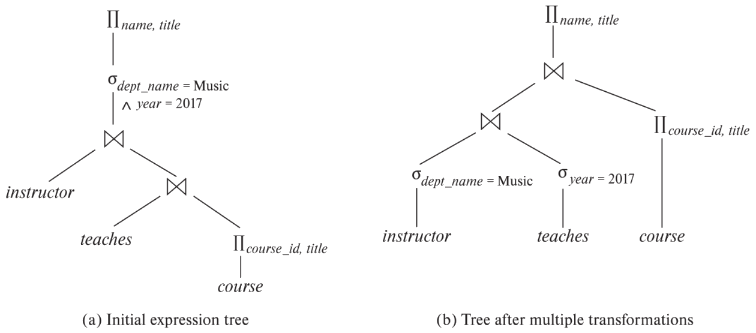
- Projection을 가능한 한 빨리 수행하면 join할 relation의 크기 감소
- Πname, title((σdept_name= “Music”(instructor)⋈teaches)⋈Πcourse_id, title(course))
- (σdept_name = “Music”(instructor)⋈teaches) 계산 시,
- schema는
(ID, name, dept_name, salary, course_id, sec_id, semester, year)
- 이 중
course_id (join용)와 name (output용)만 필요 - 동등성 규칙 8a, 8b를 사용한 projection push
- Πname, title(Πname, course_id(σdept_name= “Music”(instructor)⋈teaches))⋈Πcourse_id, title(course))
- 모든 relation r1,r2,r3에 대해 (r1⋈r2)⋈r3=r1⋈(r2⋈r3) (Join Associativity)
- 만약 r2⋈r3이 매우 크고 r1⋈r2가 작다면, (r1⋈r2)⋈r3를 선택하여 더 작은 임시 relation 계산 및 저장
- 예: Πname, title((σdept_name= “Music”(instructor)⋈teaches)⋈Πcourse_id, title(course))
- teaches⋈Πcourse_id, title(course)를 먼저 계산할 수 있으나, 첫 join 결과가 큰 relation일 가능성 높음
- Music 학부 강사 비율은 낮을 것이므로, σdept_name= “Music”(instructor)⋈teaches를 먼저 계산하는 것이 더 좋음
- Database system catalog는 다음 통계 정보 저장
- nr: relation r의 tuple 수
- br: r의 tuple을 포함하는 block 수
- lr: r의 tuple 크기
- fr: r의 blocking factor (한 block에 맞는 r의 tuple 수)
- 물리적으로 r의 tuple이 파일에 함께 저장되면
- br=⌈nr/fr⌉
- V(A, r): 속성 A에 대해 r에 나타나는 distinct 값의 수 (ΠA(r)의 크기와 동일)
- 인덱스에 대한 통계도 catalog에 유지
- fi: B+-tree 같은 tree 구조 인덱스 i의 internal node의 평균 fan-out
- HTi: 인덱스 i의 level 수 (높이). B+-tree의 경우 HTi=⌈logfi(V(A,r))⌉. Hash 인덱스는 HTi=1
- LBi: i의 가장 낮은 level의 인덱스 block 수 (leaf level block 수)
- 실제 optimizer는 종종 추가적인 통계 정보를 유지
- 대부분의 데이터베이스는 각 속성의 값 분포를 히스토그램으로 저장
- Equi-width histograms: 값의 범위를 동일한 크기의 범위로 분할
- Equi-depth histograms: 각 범위가 (거의) 동일한 수의 tuple을 갖도록 범위 분할 (더 선호됨)
- 많은 데이터베이스는 n개의 가장 빈번한 값(most-frequent values)과 그 개수를 저장
- Histogram 및 기타 통계는 보통 random sample 기반으로 계산
- 통계가 최신이 아닐 수 있음 (
analyze 명령 필요 또는 자동 재계산) - 예: relation 안의 tuple의 개수가 몇 % 변화하는 경우
- 이전 연산의 출력을 입력으로 받는 중간 연산의 비용 추정 방법?
- E1,E2,E3 통계는 있지만 E1⋈E2 통계는 없음
- 각 연산 출력에 대한 통계 값 '추정' 필요
- σA=v(r)
- nr/V(A,r): selection을 만족할 것으로 추정되는 레코드 수 (A 값이 동일한 tuple의 평균 수)
- Key 속성에 대한 동등 조건: 크기 추정 = 1
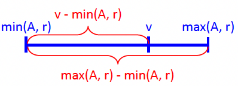
- σA≤v(r) ( σA≥v(r)도 대칭)
- 속성 값의 '균일한' 분포 가정
- c = 조건을 만족하는 추정 tuple 수
- min(A, r)과 max(A, r)을 catalog에서 사용 가능하면
- c=0, (if v<min(A, r))
- c=nr, (if v≥max(A, r))
- c=nr⋅max(A, r)−min(A, r)v−min(A, r), (otherwise)
- 히스토그램 사용 가능하면 위 추정치 개선 가능
- 통계 정보 부재 시, c=2nr로 가정
- 조건 θi의 Selectivity: relation r의 tuple이 θi를 만족할 확률
- si가 r에서 만족하는 tuple 수 (이전 슬라이드에서 추정)이면, θi의 selectivity는 si/nr
- Conjunction
- σθ1∧θ2∧⋯∧θn(r)
- 결과 tuple 추정치 (독립성 가정)
- nr⋅(nrs1)⋅(nrs2)⋯(nrsn)
- Disjunction
- σθ1∨θ2∨⋯∨θn(r)
- 추정 tuple 수
- nr(1−(1−nrs1)(1−nrs2)…(1−nrsn))
- Negation
- σ¬θ(r)
- 추정 tuple 수
- nr – (σθ(r)의 추정 tuple 수)
- 예제 Query:
student ⋈ takes - Catalog 정보
- nstudent=5000
- fstudent=50, bstudent=100
- ntakes=10000
- ftakes=25, btakes=400
- V(ID, takes)=2500 (과목을 수강한 학생은 평균 4과목 수강)
takes의 ID는 student를 참조하는 foreign key- V(ID, student)=5000 (primary key)
- Cartesian 곱 r×s는 nr⋅ns 개의 tuple 포함. 각 tuple은 lr+ls바이트
- r⋈s=r×s, (if R∩S=∅)
- R∩S가 R의 key인 경우
- s의 tuple은 r의 최대 1개 tuple과 join. ( r⋈s의 tuple 수) ≤ns
- R∩S가 S에서 R을 참조하는 foreign key인 경우: (r⋈s의 tuple 수) =ns (foreign key 제약조건 때문)
student ⋈ takes 예제: takes의 ID는 student를 참조하는 foreign key, 따라서 결과는 ntakes (10000)개의 tuple 가짐- R∩S={A}가 R 또는 S의 key가 아닌 경우
- R의 모든 tuple t가 R⋈S에서 tuple을 생성한다고 가정하면, R⋈S의 tuple 수 추정
- V(A, s)nr⋅ns
- 반대의 경우 (S 기준) 추정
- V(A, r)nr⋅ns
- 이 두 추정치 중 낮은 값이 아마도 더 정확 (join에 참여하지 않는 dangling tuple이 존재 가능하므로)
- Foreign key 정보 없이
student ⋈ takes 크기 추정 - V(ID, takes)=2500, V(ID, student)=5000
- 두 추정치
- (5000⋅10000)/2500=20000 및 (5000⋅10000)/5000=10000
- 더 낮은 추정치인 10000을 선택 (foreign key 사용한 이전 계산과 동일)
- Projection
- ΠA(r)의 추정 크기 = V(A, r)
- Set operations
- 동일 relation에 대한 selection의 union/intersection: 재작성 후 selection 크기 추정 사용 (예: σθ1(r)∪σθ2(r)→σθ1∨θ2(r))
- 다른 relation에 대한 연산
- r∪s 추정 크기 = nr+ns
- r∩s 추정 크기 = min(nr, ns)
- r−s 추정 크기 = nr
- (세 추정치 모두 부정확할 수 있으나 upper bound를 제공)
- 각 연산 결과의 attribute A에 대한 distinct 값의 수 V(A,…) 추정 필요
- Selections: σθ(r)
- θ가 A를 특정 값(예: A=3)으로 강제
- V(A, σθ(r))=1
- θ가 A를 특정 값 집합 중 하나(예: A=1∨A=3∨A=4)로 강제
- V(A, σθ(r))= (명시된 값의 수)
- θ가 A (op) v 형태
- V(A, σθ(r))≈V(A, r)⋅s (s는 selection의 selectivity)
- 그 외
- min(V(A, r), nσθ(r)) (upper bound)
- Joins: r⋈s
- A가 r의 attribute인 경우
- V(A, r⋈s)≈min(V(A, r), nr⋈s)
- Projections: ΠA(r)
- V(A, ΠA(r))=V(A, r)
- 비용 기반 optimizer: 주어진 query와 동등한 모든 query-evaluation plan 탐색, 최소 추정 비용 plan 선택
- Plan 선택 시 evaluation 기법 간 상호작용 고려 필요
- 각 연산에 대해 독립적으로 가장 저렴한 알고리즘 선택이 최적의 전체 알고리즘을 보장하지 않음
- 예: Merge-join이 hash-join보다 비싸지만, 정렬된 output 제공하여 외부 집계 비용 줄일 수 있음
- (Block) nested-loop join은 pipelining 기회 제공 가능
- 실제 query optimizer는 다음 두 접근 방식 요소 통합
- 모든 plan 탐색 후 비용 기반 방식으로 최선의 plan을 선택
- Heuristics를 사용하여 plan을 선택
- r1⋈r2⋈⋯⋈rn에 대한 최적 join-order 찾기
- (2(n−1))!/(n−1)! 개의 다른 join order 존재
- n=3일 때 12개
r1⋈(r2⋈r3)r2⋈(r1⋈r3)r3⋈(r1⋈r2)r1⋈(r3⋈r2)r2⋈(r3⋈r1)r3⋈(r2⋈r1)(r2⋈r3)⋈r1(r1⋈r3)⋈r2(r1⋈r2)⋈r3(r3⋈r2)⋈r1(r3⋈r1)⋈r2(r2⋈r1)⋈r3
- n=7일 때 665,280개, n=10일 때 1760억 개 이상
- 모든 join order 생성 불필요
- Dynamic programming 사용
- {r1, r2, …, rn}의 모든 부분집합(subset)에 대한 최소 비용 join order를 한 번만 계산하고 향후 사용 위해 저장
- 예: (r1⋈r2⋈r3)⋈r4⋈r5
- {r1, r2, r3}에 대한 최적 join order 찾으면, r4,r5와의 추가 join에 해당 order 사용
- Left-deep join tree에서 각 join의 오른쪽 입력(right-hand-side input)은 (중간 join 결과가 아닌) relation
- Pipelined evaluation에 특히 편리 (오른쪽 피연산자가 저장된 relation이므로 각 join의 입력 중 하나만 pipelined)
- System R optimizer는 left-deep join order만 고려
- 총 n! 개의 join order ( (2(n−1))!/(n−1)! 보다 훨씬 적음)
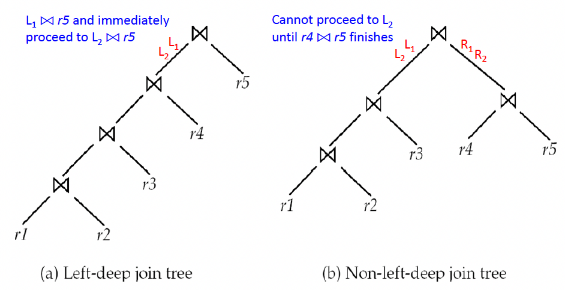
- 비용 기반 최적화는 dynamic programming 사용하더라도 비용 높음
- 시스템은 비용 기반 방식으로 선택해야 하는 대안 수를 줄이기 위해 heuristics 사용 가능
- Heuristic 최적화: 실행 성능을 (항상은 아니지만) 일반적으로 향상시키는 규칙 집합을 사용하여 query-tree 변환
- Selection 조기 수행 (tuple 수 감소)
- Projection 조기 수행 (속성 수 감소)
- 다른 유사 연산보다 가장 제한적인(가장 작은 결과 크기) selection 및 join 연산 먼저 수행
- 일부 시스템은 휴리스틱만 사용, 다른 시스템은 휴리스틱과 부분적 cost-based optimization 결합




