3 - Transformations

Outline

• 2차원 변환
  • Scaling, Rotation, Shearing, Reflection
  • Translation
• 변환의 종류
• 변환의 합성과 Homogeneous Coordinates
• 두 가지 3차원 직교 좌표계
• 3차원 Affine 변환

What is Transformation?

• Geometric Transformation
  • 기하학적 object의 위치, 방향, 크기 또는 형태를 수학적으로 변경하는 과정
    → “점들의 집합을 이동시키는 것”
  • 복잡한 장면과 애니메이션 생성을 가능하게 함
  • Computer graphics에서 필수적임
• 예시:
  • Translate
  • Rotate
  • Scale
  • Shear
  • Reflect

Transformation

• “점들의 집합을 이동시키는 것”
• Transformation T는 벡터 공간 S에 있는 임의의 입력 벡터 v를 T(v)로 사상(寫像)함
• 수식 표현: $S \rightarrow \{~ T(v) \mid v \in S ~\}$

Linear Transformation

• 행렬 곱을 통해 Transformation을 정의할 수 있음 $$ T(\mathbf{v}) = M\mathbf{v} $$
• 이는 행렬 곱셈이 선형 사상(寫像)을 나타내게 되므로
  linear transformation이라 부름
• Linear transformation은 다음 조건을 만족해야 함: $$ T(\mathbf{v}_1 + \mathbf{v}_2) \\ = T(\mathbf{v}_1) + T(\mathbf{v}_2), \quad T(c\mathbf{v}) \\ = cT(\mathbf{v}) $$
• 행렬 $M$ 또한 동일한 *선형성(linearity)*을 만족: $$ M(\mathbf{v}_1 + \mathbf{v}_2) \\ = M\mathbf{v}_1 + M\mathbf{v}_2, \quad M(c\mathbf{v}) \\ = c(M\mathbf{v}) $$

2D Linear Transformations

• 2×2 행렬은 다음과 같은 2차원 linear transformation을 표현할 수 있음:
  • uniform scaling
  • non-uniform scaling
  • rotation
  • shearing
  • reflection

2D Linear Trans. – Uniform Scaling

• x축과 y축 모두에서 동일한 비율로 확대 또는 축소 $$ \mathbf{S} = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \\ \mathbf{p} = \begin{bmatrix} x \\ y \end{bmatrix} \quad\Rightarrow\quad \mathbf{p}' = \begin{bmatrix} sx \\ sy \end{bmatrix} $$
• 예: 배율 ( s = 1.5 )인 scaling을 적용할 경우,
  $$ \begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1.5x \\ 1.5y \end{bmatrix} $$

2D Linear Trans. – Nonuniform Scaling

• x축과 y축 방향으로 서로 다른 비율로 확대 또는 축소 $$ \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} s_xx \\ s_yy \end{bmatrix} $$

(예: $s_x$ = 1.5, $s_y$ = 0.8 → $x$축 방향은 확대, $y$축 방향은 축소)

2D Linear Trans. – Rotation

• 회전은 행렬 곱으로 표현 가능하며, 따라서 선형 변환임
• 양의 각도는 반시계 방향(CCW, Counter-Clockwise)을 의미함 $$ \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \cos \theta - y \sin \theta \\ x \sin \theta + y \cos \theta \end{bmatrix} $$

(예: $\theta = 30\degree$ → 30도 반시계 회전)

Numbers in Matrices: Scaling, Rotation

• 행렬의 각 숫자는 어떤 의미를 가질까?
• 단위 벡터$([1, 0]^T, [0, 1]^T)$을 기준으로 scaling 또는 rotation 시 각각의 column vector가 변환된 축의 방향을 나타냄
• Canonical basis vectors: 직교 좌표계에서 x, y축 방향 단위 벡터
• 결과적으로, 변환된 좌표계의 축 방향을 나타냄
• 행렬의 column vector는 그 행렬의 column space를 구성하는 basis vectors
• Column space: column vector들의 선형 결합으로 표현 가능한 모든 벡터의 집합

2D Linear Trans. – Reflection

• Reflection은 non-uniform scaling의 특수한 경우로 간주할 수 있음
• 예시: $x$축 방향 reflection $$ \begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix} $$

2D Linear Trans. – Shearing

• 물체를 측면으로 밀기(push sideways)
• 예시: $x$축 기준으로 $y$에 비례하여 $x$ 이동 $$ \begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} x+ay\\ y \end{bmatrix} $$

Identity Matrix

• 아무런 변환도 수행하지 않는 행렬 → "Doing nothing" $$ \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} x\\ y \end{bmatrix} $$

(도형의 위치, 크기, 방향이 유지됨)

[Demo] 2D Linear Transformations

• integral-domain.org/lwilliams/Applets/algebra/linearTransformations.php (opens new window)
• 행렬 요소의 값을 바꿔보세요
• 다양한 변환 버튼을 눌러보세요

Quiz 1

2D Translation

• Translation은 가장 간단한 변환:
  $T(\mathbf{v}) = \mathbf{v} + \mathbf{u}$
• 역변환(Inverse):
  $T^{-1}(\mathbf{v}) = \mathbf{v} − \mathbf{u}$

(도식: $\mathbf{v}$ 벡터에서 $\mathbf{u}$만큼 이동한 결과가 $T(\mathbf{v})$)

Is translation linear transformation?

• 아니오. 선형 변환(linear transformation)이 아님

• 선형성(linearity)을 만족하지 않음:
  $$ T(\mathbf{v}_1 + \mathbf{v}_2) \neq T(\mathbf{v}_1) + T(\mathbf{v}_2) \\ T(c\mathbf{v}) \neq cT(\mathbf{v}) $$

  예:

  $$ cT(\mathbf{v}) = c(\mathbf{v} + \mathbf{b}) = c\mathbf{v} + c\mathbf{b} \\ \neq T(c\mathbf{v}) = c\mathbf{v} + \mathbf{b} $$

• 벡터 덧셈을 사용해 표현 가능:
  $$ T(\mathbf{v}) = \mathbf{v} + \mathbf{u} $$

• 선형 변환과 결합할 수 있음:
  $$ T(\mathbf{v}) = M\mathbf{v} + \mathbf{u} $$

• → Affine transformation

Let’s check again

• Linear transformation
  • Scaling, Rotation, Reflection, Shearing
  • 행렬 곱셈으로 표현 가능
    $$ T(\mathbf{v}) = \mathbf{Mv} $$
• Translation
  • 선형 변환이 아님
  • 벡터 덧셈으로 표현됨
    $$ T(\mathbf{v}) = \mathbf{v} + \mathbf{u} $$
• Affine transformation
  • 선형 변환과 translation을 결합한 형태
    $$ T(\mathbf{v}) = \mathbf{Mv} + \mathbf{u} $$

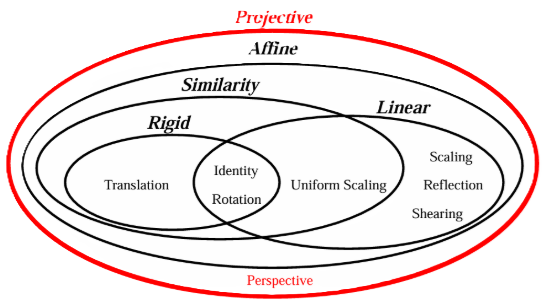
Rigid Transformations

• 모든 점 사이의 거리를 유지함 $$ |g(\mathbf{u}) - g(\mathbf{v})| = |\mathbf{u} - \mathbf{v}|, \\ \forall \mathbf{u}, \mathbf{v} \in \mathbb{R}^3 \quad (g: \text{rigid transform map}) $$
• "Handedness"를 보존함:
  • 선형 변환 중 handedness를 보존하는 회전의 조건:
    $$ g(\mathbf{u}) \times g(\mathbf{v}) = g(\mathbf{u} \times \mathbf{v}), \\ \forall \mathbf{u}, \mathbf{v} \in \mathbb{R}^3 $$
    • Reflection은 보존하지 않음
  • Translation은 방향을 바꾸지 않으므로 영향을 주지 않음
• Rigid transformation의 예:
  • Translation
  • Identity
  • Rotation
• 일부 문헌에서는 reflection을 rigid로 분류하기도 하나, 본 강의에서는 포함하지 않음

Similarity Transformations

• 각도를 보존함
• (rigid transformation도 각도 보존 포함)
• Similarity transformation의 예:
  • Translation
  • Identity
  • Rotation
  • Uniform Scaling
• 일부 문헌에서는 reflection도 포함하나, 본 강의에서는 다루지 않음

Linear Transformations

• 원점을 보존함
• 포함되는 변환들:
  • Translation
  • Identity
  • Rotation
  • Uniform Scaling
  • Scaling
  • Reflection
  • Shearing

Affine Transformations

• 평행선을 유지함
• 직선 상의 거리 비율을 유지함

Projective Transformations

• 직선을 보존함

Composition of Transformations

• 어떤 물체에 T 변환을 적용한 후, S 변환을 추가 적용: $$ \mathbf{p} \rightarrow T(\mathbf{p}) \rightarrow S(T(\mathbf{p})) = (S \circ T)(\mathbf{p}) $$
• 2D linear transformation의 합성은
  2×2 행렬 곱셈으로 표현 가능: $$ T(\mathbf{p}) = M_T \mathbf{p}; \quad S(\mathbf{p}) = M_S \mathbf{p} $$ $$ (S \circ T)(\mathbf{p}) = M_S M_T \mathbf{p} \\ = (M_S M_T)\mathbf{p} = M_S (M_T \mathbf{p}) $$

Order Matters!

• 행렬 곱셈은 결합법칙은 성립하지만 교환법칙은 성립하지 않음: $$ (AB)C = A(BC) \\ AB \ne BA $$
• 따라서, 변환의 적용 순서가 매우 중요함

(예: Scale → Rotate vs Rotate → Scale 결과가 다름)

[Demo] Composition of Linear Transformations

• integral-domain.org/lwilliams/Applets/algebra/linearTransformations.php (opens new window)
• identity matrix로 초기화 (1 0 0 1 입력)
• "Compose Transformations" 버튼 클릭
• 두 개의 변환을 서로 다른 순서로 적용해보기

Problems when handling Translation as Vector Addition

• 선형 변환(회전, 스케일 등)과 translation을
  일관된 방식으로 표현할 수 없음
• Affine 변환의 합성은 복잡해짐: $$ T(\mathbf{p}) = M_T \mathbf{p} + \mathbf{u}_T \\ S(\mathbf{p}) = M_S \mathbf{p} + \mathbf{u}_S $$ $$ (S \circ T)(\mathbf{p}) = M_S(M_T \mathbf{p} + \mathbf{u}_T) + \mathbf{u}_S \\ = (M_S M_T) \mathbf{p} + (M_S \mathbf{u}_T + \mathbf{u}_S) $$
• 더 깔끔한 표현 방식이 필요함
  → Homogeneous coordinates

Homogeneous Coordinates

• 핵심 아이디어: 2D 점을 3D 좌표계 상에 표현
• 벡터에는 추가 성분($w$), 행렬에는 추가 행/열을 추가
  • 점에는 항상 $w = 1$
  • 2D 점 $[x,~y]^T → [x,~y,~1]^T$
• 2D linear transformation의 표현: $$ \begin{bmatrix} a & b & 0 \\ c & d & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \\ 1 \end{bmatrix} $$
• 2D translation의 표현: $$ \begin{bmatrix} 1 & 0 & t \\ 0 & 1 & s \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t \\ y + s \\ 1 \end{bmatrix} $$
• 2D affine transformation의 표현: $$ \begin{bmatrix} m_{11} & m_{12} & u_x \\ m_{21} & m_{22} & u_y \\ 0 & 0 & 1 \end{bmatrix} $$
• Affine transformation 합성은 3×3 행렬 곱셈으로 간단하게 처리 가능: $$ T(\mathbf{p}) = M_T \mathbf{p} + \mathbf{u}_T \\ S(\mathbf{p}) = M_S \mathbf{p} + \mathbf{u}_S $$ → block 행렬 표현: $$ T(\mathbf{p}) = \begin{bmatrix} M_T & \mathbf{u}_T \\ 0 & 1 \end{bmatrix}, \\ S(\mathbf{p}) = \begin{bmatrix} M_S & \mathbf{u}_S \\ 0 & 1 \end{bmatrix} $$ $$ (S \circ T)(\mathbf{p}) \\ = \begin{bmatrix} M_S & \mathbf{u}_S \\ 0 & 1 \end{bmatrix} \begin{bmatrix} M_T & \mathbf{u}_T \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{p} \\ 1 \end{bmatrix} \\ = \begin{bmatrix} (M_S M_T) \mathbf{p} + (M_S \mathbf{u}_T + \mathbf{u}_S) \\ 1 \end{bmatrix} $$
• 결과는 이전 방식과 같지만, 훨씬 간단하고 깔끔함

cf. 기존 표현과 비교:
$(S \circ T)(\mathbf{p}) = M_S(M_T \mathbf{p} + \mathbf{u}_T) + \mathbf{u}_S$
$= (M_S M_T)\mathbf{p} + (M_S \mathbf{u}_T + \mathbf{u}_S)$

[Demo] Composition of Affine Transformations in Homogeneous Coordinates

• observablehq.com/@esperanc/transformation-demo (opens new window)
• ‘+’ 버튼으로 다양한 순서의 translation 및 linear transformation 추가
• 슬라이더로 행렬 값의 변화와 도형 변형 확인
• 주의: 마지막에 추가된 변환이 가장 먼저 적용됨

Summary: Homogeneous Coordinates in 2D

• 2D 점에는 $(x,~y)^T$ 대신 $(x,~y,~1)^T$ 사용
• 2D linear transformation에는 2×2 행렬 대신 3×3 행렬 사용
• 2D translation에도 벡터 덧셈 대신 3×3 행렬 사용

→ linear transformation과 translation을 일관된 방식으로 처리할 수 있음!

Quiz 2

Now, Let’s go to the 3D world!

• Coordinate system (좌표계)
  • Cartesian coordinate system (직교좌표계)
    • 2D 좌표계 → z축이 포함된 3D 좌표계로 확장됨

Right-Handed and Left-Handed Coordinate Systems

• 우리가 사용하는 시스템: Right-handed Cartesian Coordinates

항목	Right-handed	Left-handed
회전 방향	축 기준 반시계 방향	축 기준 시계 방향
사용 예시	OpenGL, Maya, Houdini, AutoCAD, Physics & Math	DirectX, Unity, Unreal 등

(이미지: 오른손 법칙과 왼손 법칙 설명)

Point Representations in Cartesian & Homogeneous Coordinate System

A 2D point is represented as:

• Cartesian coordinate system: $$ \begin{bmatrix} p_x \\ p_y \end{bmatrix} $$
• Homogeneous coordinate system: $$ \begin{bmatrix} p_x \\ p_y \\ 1 \end{bmatrix} $$

A 3D point is represented as:

• Cartesian coordinate system: $$ \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} $$
• Homogeneous coordinate system: $$ \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} $$

Review of Linear Transformations in 2D

• 2D에서의 선형 변환은 다음과 같은 행렬 곱셈으로 표현됨:

2x2 matrix (in Cartesian coordinates):

$$ \begin{bmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{bmatrix} \begin{bmatrix} p_x \\ p_y \end{bmatrix} $$

or

3x3 matrix (in homogeneous coordinates):

$$ \begin{bmatrix} m_{11} & m_{12} & 0 \\ m_{21} & m_{22} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ 1 \end{bmatrix} $$

Linear Transformations in 3D

• 3D에서의 선형 변환은 다음 행렬 곱셈으로 표현됨:

  • 3x3 matrix (in Cartesian coordinates)
    또는
  • 4x4 matrix (in homogeneous coordinates)

  $$ \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} \\ \text{or}\ \\ \begin{bmatrix} m_{11} & m_{12} & m_{13} & 0 \\ m_{21} & m_{22} & m_{23} & 0 \\ m_{31} & m_{32} & m_{33} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} $$

Linear Transformations in 3D

Scaling (크기 조절):

$$ S_s = \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & S_z \end{bmatrix} \quad\text{(3D)} \\ S_s = \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad\text{(3D-H)} $$

Shear (in $x$, based on $z$ position):

$$ H_{x,d} = \begin{bmatrix} 1 & d_y & d_z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ \text{or} \\ H_{x,d} = \begin{bmatrix} 1 & d_y & d_z & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

Linear Transformations in 3D

Rotation about $x$-axis:

$$ R_{x,\theta} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} $$

Rotation about $y$-axis:

$$ R_{y,\theta} = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix} $$

Rotation about $z$-axis:

$$ R_{z,\theta} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

(오른손 법칙에 따라 z축을 기준으로 위에서 아래로 보는 시점에서 반시계 방향 회전)

Review of Translations in 2D

• 2D에서의 Translation은 다음 두 방식으로 표현 가능:

Vector addition (in Cartesian coordinates):

$$ \begin{bmatrix} p_x \\ p_y \end{bmatrix} + \begin{bmatrix} u_x \\ u_y \end{bmatrix} $$

Matrix multiplication (in homogeneous coordinates):

$$ \begin{bmatrix} 1 & 0 & u_x \\ 0 & 1 & u_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ 1 \end{bmatrix} $$

Translations in 3D

• 3D에서의 Translation도 유사하게 표현 가능:

Vector addition (Cartesian coordinates):

$$ \begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} + \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix} $$

Matrix multiplication (homogeneous coordinates):

$$ \begin{bmatrix} 1 & 0 & 0 & u_x \\ 0 & 1 & 0 & u_y \\ 0 & 0 & 1 & u_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} $$

Review of Affine Transformations in 2D

• Homogeneous coordinates에서는 2D affine transformation을 3×3 행렬 곱으로 표현할 수 있음:

$$ \begin{bmatrix} m_{11} & m_{12} & u_x \\ m_{21} & m_{22} & u_y \\ 0 & 0 & 1 \end{bmatrix} $$

Affine Transformations in 3D

• Homogeneous coordinates에서는 3D affine transformation을
  4×4 행렬 곱으로 표현할 수 있음:

$$ \begin{bmatrix} m_{11} & m_{12} & m_{13} & u_x \\ m_{21} & m_{22} & m_{23} & u_y \\ m_{31} & m_{32} & m_{33} & u_z \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

Summary: Affine Transformation

• $\mathbf{p}$라는 점 집합에 대해 affine transformation $\mathbf{M}$을 적용하면: $$ \mathbf{M} = \begin{bmatrix} m_{11} & m_{12} & m_{13} & u_1 \\ m_{21} & m_{22} & m_{23} & u_2 \\ m_{31} & m_{32} & m_{33} & u_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

$$ \mathbf{p}_i' \leftarrow \mathbf{M} \mathbf{p}_i $$

$$ \mathbf{p}_1' \leftarrow \mathbf{M} \mathbf{p}_1 \\ \mathbf{p}_2' \leftarrow \mathbf{M} \mathbf{p}_2 \\ \mathbf{p}_3' \leftarrow \mathbf{M} \mathbf{p}_3 \\ \dots \\ \mathbf{p}_N' \leftarrow \mathbf{M} \mathbf{p}_N $$

Summary: Composition of Affine Transformations

• 여러 개의 affine transformation (예: M₁, M₂)을 순차적으로 적용할 수 있음
• 각 점마다 개별적으로:

$$ \mathbf{p}_i'' \leftarrow \mathbf{M}_2 \mathbf{M}_1 \mathbf{p}_i $$

$$ \mathbf{p}_1'' \leftarrow \mathbf{M}_2 \mathbf{M}_1 \mathbf{p}_1 \\ \mathbf{p}_2'' \leftarrow \mathbf{M}_2 \mathbf{M}_1 \mathbf{p}_2 \\ \mathbf{p}_3'' \leftarrow \mathbf{M}_2 \mathbf{M}_1 \mathbf{p}_3 \\ \dots \\ \mathbf{p}_N'' \leftarrow \mathbf{M}_2 \mathbf{M}_1 \mathbf{p}_N $$

---

BUILT WITH

All trademarks and logos are property of their respective owners.
© 2025 kmbzn · MIT License
Based on © 2020 Gyoogle · MIT License